Feux de forêt

Dans cet article, nous allons examiner un modèle simple représentant la propagation d’un feu de forêt. Ce modèle a été adapté à partir d’un exemple disponible sur le site officiel de NetLogo. Nous représentons une zone forestière en utilisant des carrés verts pour les arbres et des carrés noirs pour les rochers. L’image ci-dessous illustre un tel morceau de forêt.

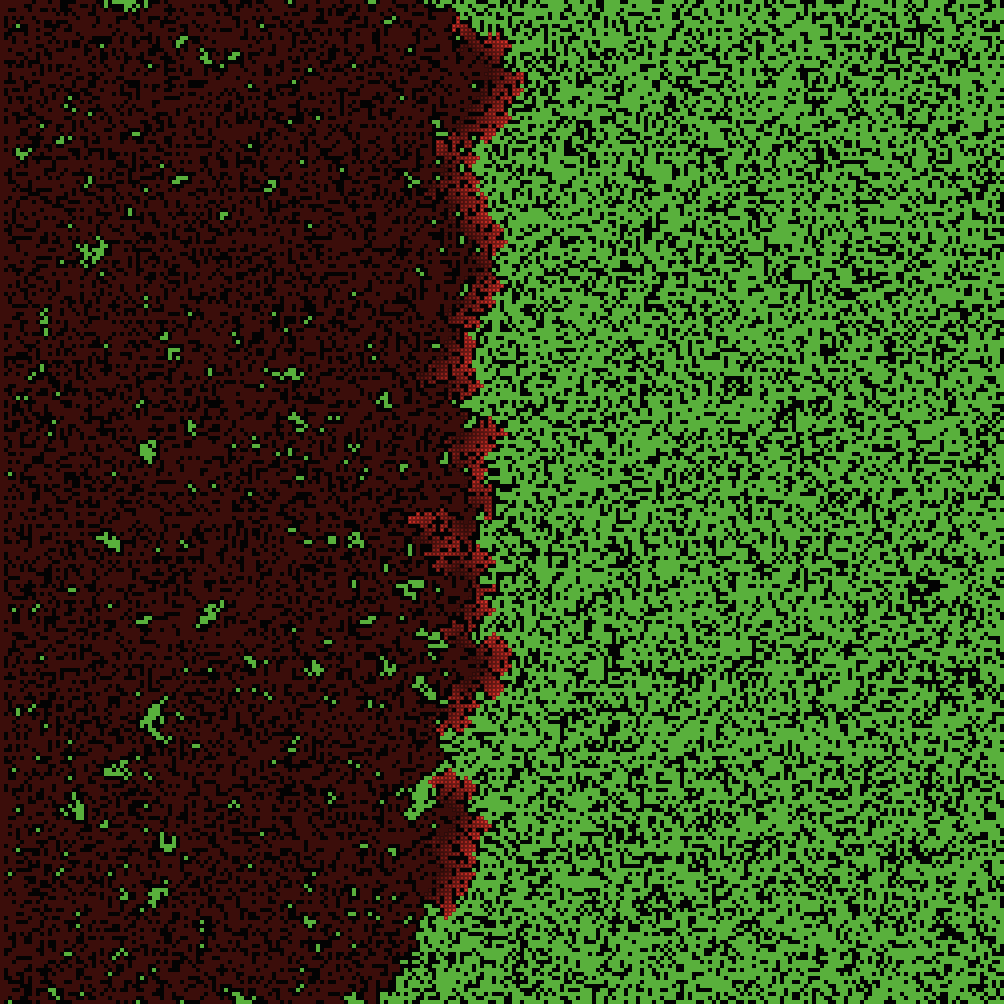
Notre objectif est de modéliser la propagation d’un feu de forêt. Au départ, nous allumons un feu sur le côté gauche de la forêt, représenté par des carrés rouges. Le feu ne peut bruler que des arbres (carrés verts) et les carrés noirs agissent comme des barrières empêchant le feu de se propager. Lorsqu’un arbre est brûlé, son carré devient brun. L’image ci-dessous illustre un exemple de propagation du feu.

Ici, vous pouvez lancer des simulations pour voir par vous-même comment les incendies se propagent. Vous pouvez choisir la densité initiale des arbres (la proportion de carrés verts par rapport au nombre total de carrés). Cliquez ensuite sur “configuration” pour initialiser la simulation et sur “lancer” pour la démarrer.

Vous pouvez relancer la simulation avec une densité initiale d’arbres différente. Sélectionnez la densité initiale des arbres et cliquez à nouveau sur “configuration” et sur “lancer”.

On constate que selon la densité des arbres (la proportion de carrés verts), les feux peuvent se propager plus ou moins. En effet, pour une faible densité, le feu s’arrête rapidement. A l’inverse, lorsque la densité d’arbres est suffisamment importante, le feu se propage vers la droite de la forêt.

Maintenant, quelle densité d’arbres choisirez-vous pour maximiser la production de bois sans risquer qu’un incendie ne brûle la majeure partie de la forêt ? Essayez de recommencer la simulation (configuration) avec différentes densités pour maximiser la valeur finale de la “densité d’arbres encore vivants”.

Afin d’estimer la valeur optimale, j’ai répété l’expérience 10 fois pour chaque densité. Sur le graphique ci-dessous, chaque croix représente la valeur finale d’une expérience numérique. La ligne est la moyenne des différentes simulations. Tout d’abord, on constate que la densité d’arbres brûlés augmente avec la densité initiale. Ceci est logique : plus il y a d’arbres présents, plus il y a d’arbres à brûler. Cependant, la relation n’est pas linéaire, c’est-à-dire qu’il ne s’agit pas d’une ligne droite. Pour les faibles densités (inférieures à 50 %), presque aucun arbre ne brûle car le feu ne peut pas se propager. Cependant, à une valeur critique d’environ 0,59, le feu peut se propager à l’ensemble de la forêt et la plupart des arbres brûlent. Ce point a été estimé récemment par Newman and Ziff. Au-delà de ce point, l’augmentation de la densité des arbres initiaux augmentera la densité des arbres brûlés de manière similaire, puisque le feu se propage presque partout et que la plupart des arbres brûlent.

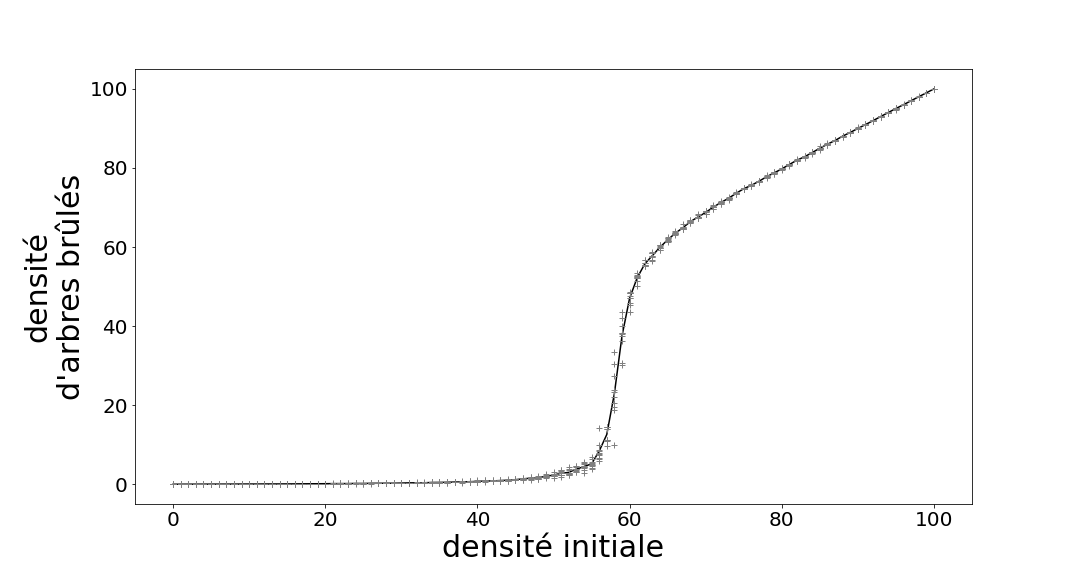
Rappelons l’objectif de notre modèle : nous voulons savoir quelle est la densité optimale d’arbres pour maximiser le nombre d’arbres sans risquer qu’ils brûlent. Nous avons donc besoin de représenter la densité d’arbres encore vivants en fonction de la densité initiale. Or, nous pouvons estimer cette valeur à environ 55%.

Vous vous demandez peut-être si ce modèle peut réellement être utilisé pour prévenir les incendies de forêt. Je pense que ce modèle est trop simpliste et repose sur des hypothèses qui ne sont pas établies empiriquement. Par conséquent, connaître la valeur précise du point critique n’est peut-être pas pertinent. Cependant, ce qui est plus intéressant, c’est le résultat qualitatif selon lequel la densité des arbres brûlés et des arbres initiaux n’est pas linéaire. Plus précisément, il existe un point critique où la dynamique change.

Plus important encore, le concept de “paramètre critique” peut être appliqué dans de nombreux domaines différents. La théorie utilisée ici est la théorie de la percolation, qui est employée dans la science des matériaux, la chimie ou la physique.