Modèle épidémique

Dans ce billet, j’aimerais expliquer pourquoi les mathématiciens aiment utiliser des équations. Pour illustrer cela, nous allons explorer le modèle SIR, couramment utilisé pour simuler les épidémies. Il existe plusieurs façons de formuler un modèle, et nous présentons ici un modèle basé sur des agents. Le code a été adapté à partir d’un modèle NetLogo précédent.

Pour lancer le modèle, cliquez sur “configurer” puis sur “lancer”. Vous pouvez redémarrer la simulation en cliquant à nouveau sur “configurer”, et vous pouvez également ajuster différents paramètres avant de configurer la simulation. Dans cette simulation, chaque agent est représenté individuellement. Dans les illustrations graphiques, vous pouvez observer trois types d’individus différents : ceux en rouge sont infectés par un virus, ceux en vert sont sensibles à l’infection et ceux en gris ont guéri.

Ce modèle basé sur des agents fournit des résultats intéressants. Le résultat n’est pas une prédiction parfaite de l’avenir, mais il peut être utilisé pour comprendre la dynamique de l’épidémie. Nous voulons maintenant simplifier ce modèle et en extraire autant de résultats que possible. Une façon de procéder consiste à exécuter les simulations précédentes avec de nombreuses valeurs de paramètres différentes et à observer les divers résultats. Une approche plus élégante consiste à traduire ce modèle en équations. Le système d’équations suivant est à peu près similaire au modèle précédent, où S, I et R représentent respectivement les individus sensibles, infectés et guéris. Beta est le taux de transmission et gamma le taux de guérison.

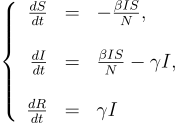
Il est maintenant plus facile d’étudier l’influence des différents paramètres sur les solutions du système d’équations. Ci-dessous, vous pouvez modifier directement les valeurs des paramètres pour voir l’impact sur l’évolution de l’épidémie.