Epidemic model

In this post, I would like to explain why mathematicians like using equations. To illustrate this, we will explore the SIR model, commonly employed to simulate epidemics. There are various ways to formulate a model, and here we present an agent-based model. The code has been adapted from a previous NetLogo model.

To run the model, click on “setup” and then on “go.” You can restart the simulation by clicking again on “setup,” and you can also adjust different parameters before setting up the simulation. In this simulation, each agent is represented individually. In the graphical illustrations, you can observe three different types of individuals: those in red are infected by a virus, those in green are susceptible to infection, and those in grey have recovered.

This agent-based model provides interesting results. The output is not a perfect prediction of the future, but it can be used to understand the dynamics of the epidemic. Now, we want to simplify this model and extract as many results as possible. One way is to run the previous simulations with many different parameter values and observe the various outputs. A more elegant approach is to translate this model into equations. The following system of equations is roughly similar to the previous model, where S, I, and R represent susceptible, infected, and recovered individuals (respectively). Beta is the transmission rate, and gamma is the recovery rate.

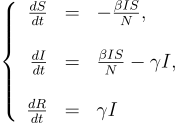
It is now easier to study the influence of the different parameters on the solutions of the system of equations. Below, you can directly change the parameter values to see the impact on the epidemic evolution.